One of the first questions when planning an RC snow cat is: "Which motor should I choose?" or "Is this or that motor sufficient for my snow cat?". Here are the physical basics.

 

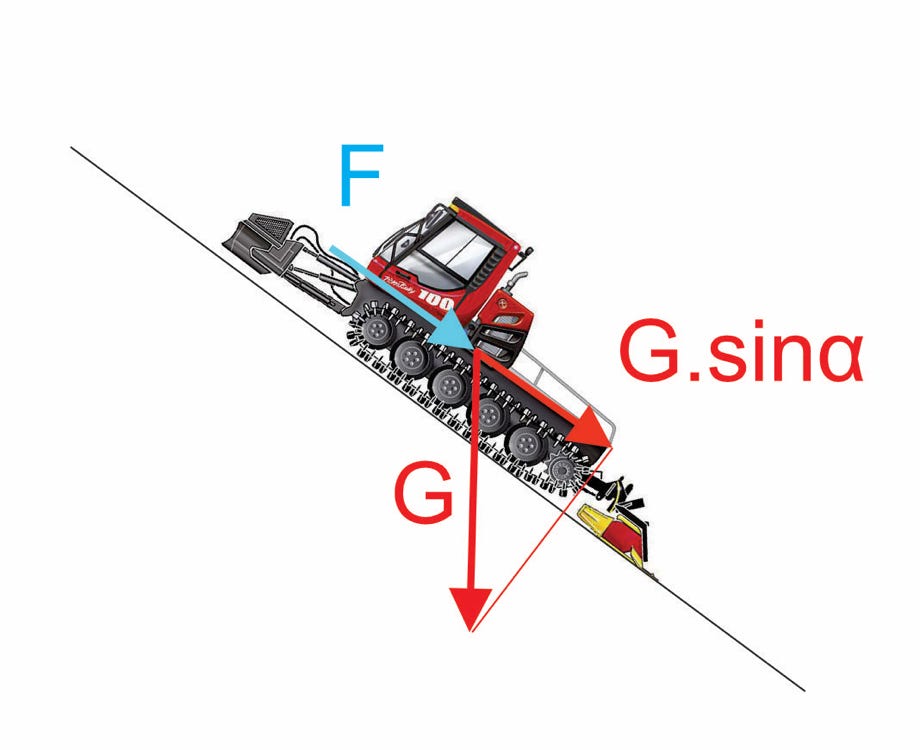
These are the forces acting on a snow cat when climbing a hill at constant speed.

 

G = weight of the snow cat, acts downwards

G * sin alpha = weight portion acting against driving direction, alpha = gradient angle (slope)

F = driving resistance of the snow cat, i.e. resistances in powertrain and snow

 

The weight of the snow cat can easily be determined using a scale. The driving resistance is a different story. Here  we did measurements. The Scaleart Commander transmitter shows the actual power consumption by telemetry on the display. This can be used to calculate the resistance. Our PB600 with a Graupner chassis needs about 6 Ampere at 7 Volt on a plain deep snow surface (see photo). The efficiency of the original Graupner motor is rather low with about 50%. With this the driving resistance is calculated as about 21 Watt. This already includes the losses in the gear box. 

 

Power = Volt * Ampere, in this case 6 x 7 = 42 Watt, 42 x 0.5 = 21 Watt

 

For the calculation example we took a typical 1:12 snow cat with a weight of 5 kg (= 49 N).

For the driving resistance we use the measured 21 Watt. The velocity is 0.5 m/sec, which corresponds with 21.6 km/h of the original. Gradient angle = 45°, which is a 100% grade and very steep. Here even the original would not be able to climb without a winch. The sinus of 45° = 0.7

 

power = force x velocity (instead of "x" for "times" the "*" is often used in formulas)

power = G * sin alpha * v + driving resistance power

power = 49 * 0.7 * 0.5 + 21 = 38 Watt

 

Torque is defined as: power = torque * rotational speed, which yields: torque = power / 2*Pi*speed, whereas the speed has to be given in revolutions/sec. 

With a for all scales valid speed of the driving sprocket of app. 240 R/min (= 4 R/sec) the moment is calculated as 38 / (2 * 3.14 * 4) = 1.5 Nm.

 

The engine torque would be these 1.5 Nm divided by the gear box ratio. For example for a 1:25 gear box this would be 0.06 Nm or 6 Ncm. As we are using 2 motors, each motor only has to achieve half of this torque, which is 3 Ncm. 

 

The driving resistance will of course be different depending on the motor and gear box, and possibly even lower than the already rather old Graupner chassis. Measurements at our PB400 ParkPro with highly efficient Maxon motor-gearboxes and a Pistenking flexible shaft drive yielded about the same power demand from the battery of 45 Watt. But with an efficiency of 90% about 40 Watt are used for driving power. This is almost double the amount of the Graupner. But the model is heavier and the tracks are wider. 

 

Also one would possibly not be able to climb up a 100% grade. So this is also a worst case assumption. This means that the calculated numbers are rather on the safe side.